Degree Day
Temperature controls the developmental rate of many organisms. Plants and invertebrate animals, including insects and nematodes, require a certain amount of heat to develop from one point in their life cycles to another. This measure of accumulated heat is known as physiological time or thermal time. Theoretically, physiological time or thermal time can provide a common reference for the development of organisms. The amount of heat required to complete a given organism's development does not vary—the combination of temperature (between thresholds) and time will always be the same. Physiological time or thermal time are often expressed and approximated in units called degree-days (°D).
Developmental Thresholds
Upper and lower developmental thresholds have been determined for some organisms through carefully controlled laboratory and field experiments. The lower developmental threshold for an organism is the temperature below which development stops. The lower threshold is determined by the organism's physiology. It is independent of the method used to calculate degree-days. For example, the lower developmental threshold is 15°C and the upper developmental threshold is 35°C for potential dengue carrier mosquito Aedes aegypti. Thresholds vary with different organisms. The upper developmental threshold is the temperature above which the rate of growth or development begins to decrease or stop as determined by the cutoff method. The physiological interpretation of the upper threshold is dependent on the cutoff method.
Degree-day calculations and accumulations
Degree-day calculations are based on the area under the diurnal temperature curve and between the thresholds. For a site with maximum and minimum temperatures data available, the different methods for calculating degree-days are single sine, double sine, single triangle, and double triangle. From the simplest to the most mathematically complex, these are: single triangle, double triangle, single sine, and double sine. All of these are linear methods because the rate of development is presumed to be a straight line directly related to temperature.
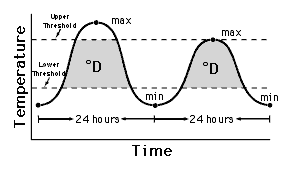
Degree day thresholds and accumulated degree-days
SimClim provides two degree day models. The first is a spatial model which calculates degree day from monthly mean temperature data using a method described in Carter et al. (1991). The second is a site specific model which calculates degree day from daily time series of maximum and minimum temperatures. The method has been described in detail by Baskerville & Emin (1969), (Andrewartha & Birch (1973), (Allen (1976), and (Wilson & Barnett (1983).
Degree Days - Cutoff Methods
The cutoff method refers to the manner in which the degree-day calculation area will be modified in relation to the upper threshold.
There are three cutoff methods - horizontal, vertical, and intermediate—to be used in conjunction with the sine and triangle calculation methods:
- Horizontal cutoff method assumes that development continues at a constant rate at temperatures in excess of the upper threshold. Mathematically, the area above the upper threshold is subtracted from the area above the lower threshold.
- Intermediate cutoff method assumes that development slows, but does not stop, at temperatures above the upper threshold. Mathematically, the area above the upper threshold is subtracted twice from the area above the lower threshold.
- Vertical cutoff method assumes that no development occurs when a temperature is above the upper threshold
Degree Days - Calculation Methods
The single triangle method draws a straight line between a day's minimum temperature and maximum temperature, assumes the next day's minimum temperature is the same, and draws another line to that point, forming two sides of a triangle. This method assumes the temperature curve is symmetrical around the maximum temperature. Degree-days are estimated by calculating the area within the triangle and between the thresholds.
The double triangle method draws a straight line between a daily minimum and maximum temperature, and another line vertically through the maximum temperature, forming two sides of a triangle. Degree-days are estimated by calculating the area within the triangle and between the thresholds. The second 12-hour period uses the same configuration with the minimum temperature of the following day. Degree-days for the day are the sum of the degree-days for the two half-days.
The single sine method uses a day's minimum and maximum temperatures to produce a sine curve over a 24-hour period, and then estimates degree-days for that day by calculating the area above the threshold and below the curve. This method assumes the temperature curve is symmetrical around the maximum temperature.
The double sine method fits a sine curve from the minimum temperature of the day to the maximum temperature of the day and then fits a separate sine curve from the maximum temperature of the day to the minimum temperature of the next day. Degree-days for the day are the sum of the degree-days for the two half-days.